The LRS Polarimeter

Due to its axis fault the spectro-polarimetry is, at the moment not available.
PAOLO is a polarimeter designed to work at a Nasmith focus of the TNG. This is a configuration implying a very careful calibration procedure which has been demonstrated to be feasible at TNG by members of our team (Giro et al. 2003, SPIE, 4843, 456) and in other telescopes with similar configurations (e.g. Tinbergen 2007, PASP 119, 1371; Joos et al. 2008, SPIE, 7016, 48; Witzel et al. 2011, A&A, 525, 130).
Typically polarimetric devices are placed on Cassegrain focus to avoid folding mirrors which modify the incoming light beam polarization state. In alt-azimuth telescopes, as the TNG, the Nasmyth focus is a suitable focal plane to reduce mechanical instrument complexity and costs. This optical configuration permits to design instruments always oriented in the same way respect to the gravity with obvious advantages in mass distributions, constrains in mechanics and flexures diminishing. On the other hand, observations performed with Nasmyth instruments are affected by strong and variable telescope polarisation. The Nasmyth mirror M3 deflects the light by 90◦ to the Nasmyth focus and introduces polarisation. Metallic mirrors introduce polarisation dependent on the surface coatings, the incidence angle (45◦ for M3) and the wavelength. Although the induced polarisation is intrinsically not dependent on the pointing direction of the telescope (always 45◦ for M3) the measured polarisation directions in a Nasmyth instrument depend strongly on the elevation of the target because the induced polarisation due to M3 is decoupled from the field. Thus, the polarisation breakdown into Stokes components is variable (dependent on pointing direction). Due to the mentioned reasons one aims to get the polarimetric data reduction integrated in a pipeline with a polarimetric instrument model based on Mueller matrices describing all polarimetric effects from the sky to the polarimetric analyzing system.
Using Muller theory, folding mirrors reflections and orientations are represented by a Matrix Mt which describe the behavior telescope polarization. If S = [I, Q, U, V ] represents the Stokes vector for the incoming light beam and S′ = [I′, Q′, U′, V ′] represents the Stokes vector for the out-coming light beam from the Nasmyth focal plane, then S′ = Mt ×S (Eq.1).
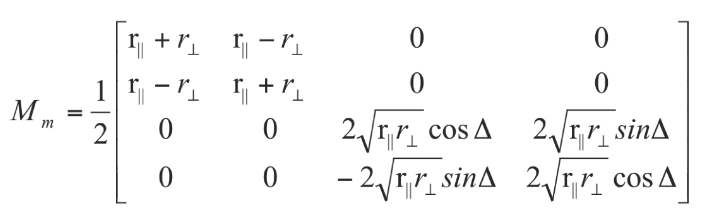
In some more detail (see Giro et al. for a complete treatment), we have to consider the reflection of the metallic surfaces of the mirrors. The electric vector of an incident electromagnetic wave on a metallic surface can be resolved into two components, one in the plane of incidence and the other perpendicular to it. The reflectivity for these two components is different. Another effect introduced by metallic reflection is a phase difference between the two electric field components. The effects of the phase shift and of the differences in reflection coefficients can be summarized using the Muller matrix for a partial polarizer combined with the Muller matrix for a retarder (see figure on the left).
A subsequent step requires to take into account different orientations of the mirror, plane of incidence not parallel to the fast axis of the polarizer/retarder. To this aim we must apply a rotation to the matrix to derive the metallic mirror matrix, Mmθ for any angle θ. Each metallic reflection can be taken in account with its Muller matrix and therefore, finally, we can compute the matrix Mt as a product of the pertinent matrix for each surface:
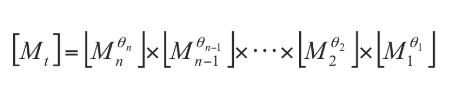
In principle polarisation due to the primary and secondary mirror is null as a consequence of the axial symmetry of reflections. If any, such a polarisation will depend on the telescope pointing exactly as M3 polarisation does and determining the Muller matrix coefficients we will indeed obtain the final contribution of two processes.
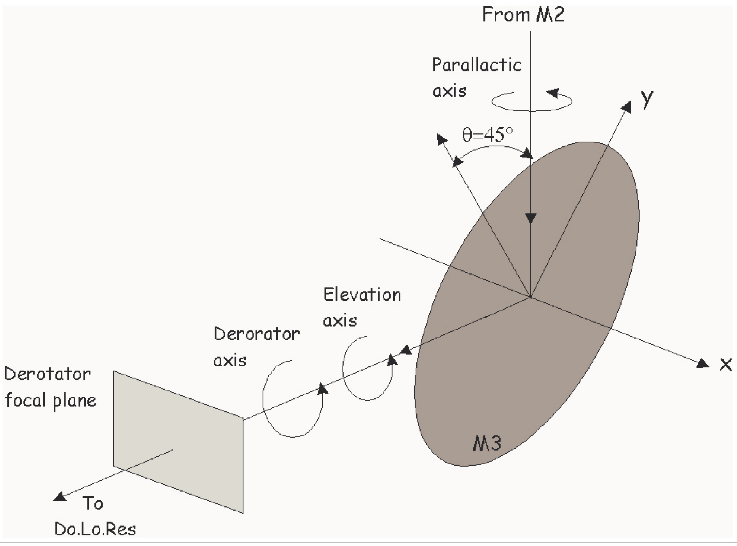
In the following plot we show the relative orientations between folding mirror, focal plane and telescope at the TNG. In order to derive the Mt matrix for the TNG system we must consider the relative positions between telescope orientation, M3 and the derotator focal plane. Because an alt-azimuth mount causes field rotation the relative orientations between the sky reference frame, typically oriented as the equatorial reference frame, and M3 reference frame are function of telescope pointing. Because M3 is co-moving with the elevation axis any change in the elevation position is reflected as a change in the orientation of M3 respect to the derotator focal plane. Summarizing there are three rotational axes parallel to the optical axis which can independently move: 1) the parallactic axis which defines the rotational axis of the equatorial reference frame respect to the telescope frame (alt-azimuth), 2) the telescope elevation axis, 3) the derotator axis designed to compensate the other two rotations at the focal plane:
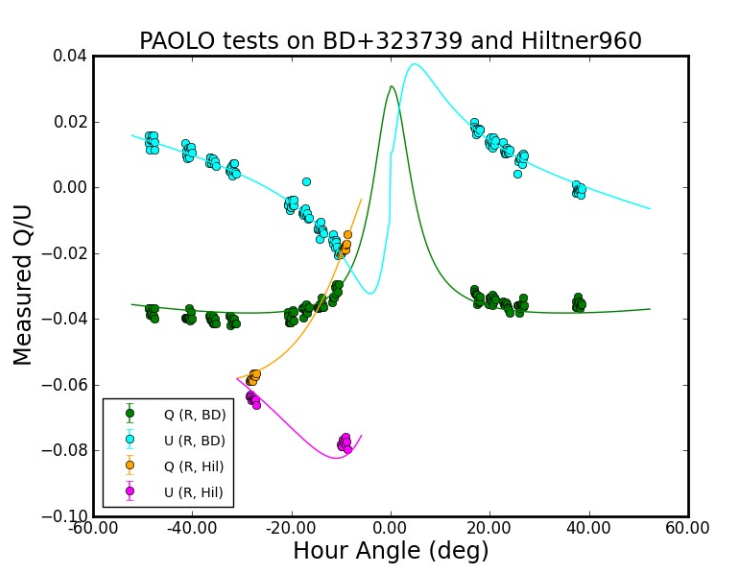
Therefore, in order to derive an accurate model for the instrumental polarization it is needed to observe a suitable set of polarized and non-polarized standard stars under different configurations. each observation it is possible to derive a set of Stokes parameters for the input data and for the output (i.e. measured, S and S′). With a suitable minimization technique one can derive best-fit parameters for the telescope Mueller matrix at various wavelengths both for imaging- and spectra-polarimetry. An example of the result of this procedure obtained during calibration is reported below. Points refer to Stokes Q and U parameters computed for an unpolarized and a polarized standard star, while lines are the appropriate model for the PAOLO instrumental polarization. Tests as the one reported below show that an accuracy of 0.3% or better is reachable.
For any further information please refer to the PAOLO project web page, the paper soon published in the Astronomical Nachriechten or feel free to contact the PI: Stefano Covino.
Last modification: Sept 17, 2012.
PAOLO is a project funded by INAF under grant TECHNO-PRIN 2009.
For any comments please contact Luca Di Fabrizio.

